Boundary Value Problems in Ellipsoidal Geometry and Applications

Introduction

The field of Mathematics is foundational to solving complex problems in science, engineering, and technology. One critical area of research involves boundary value problems (BVPs) in ellipsoidal geometry, which have far-reaching applications across disciplines. The recent study titled “Boundary Value Problems in Ellipsoidal Geometry and Applications” presents significant advancements in this domain, focusing on solving real-world challenges through mathematical models.

This blog post delves into the study’s key findings and explores how Mathematics continues to play a pivotal role in addressing boundary value problems, particularly in fields like Electroencephalography (EEG), Magnetoencephalography (MEG), creeping hydrodynamics, and electromagnetic scattering.

Explore the full study: Full Text | PDF

What Are Boundary Value Problems in Ellipsoidal Geometry?

Boundary value problems involve finding solutions to differential equations that satisfy specific conditions on the boundaries of a domain. In ellipsoidal geometry, the domain is represented by a three-dimensional ellipsoid, which provides a more realistic model for many natural and engineered systems compared to simpler spherical or cylindrical shapes.

The study emphasizes that solving BVPs in ellipsoidal geometry requires advanced mathematical techniques, including:

• Ellipsoidal Harmonics: Functions that are solutions to Laplace’s equation in ellipsoidal coordinates.
• Lamé Functions: Special functions used to solve differential equations in ellipsoidal coordinates.
• Elliptic Integrals: Integrals that arise in the computation of arc lengths of ellipses.

These mathematical tools are essential for tackling complex boundary value problems across various scientific and technological fields.

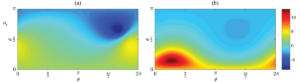Figure 1: The surface potential ue that originates from a three-shell model for an arbitrarily orientated dipole and different dipole settings (a) and (b) for several angles of observation θ and φ.

Applications of Boundary Value Problems in Mathematics

The study outlines three major application areas where boundary value problems in ellipsoidal geometry have significant practical relevance:

1. Electroencephalography (EEG) and Magnetoencephalography (MEG)
2. Creeping Hydrodynamics (Stokes Flow)
3. Identification of Metallic Bodies in Conductive and Lossless Media

Let’s explore each of these applications in detail.

1. Electroencephalography (EEG) and Magnetoencephalography (MEG)

EEG and MEG are non-invasive methods used to study brain activity by measuring electrical and magnetic fields, respectively. The study highlights that the human head can be approximated by an ellipsoid, making ellipsoidal boundary value problems highly relevant in brain imaging research.

In EEG, electrodes placed on the scalp record electrical potentials generated by neuronal activity. In MEG, superconducting quantum interference devices (SQUIDs) measure the magnetic fields produced by these currents.

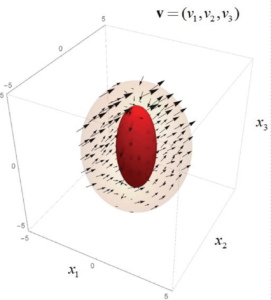Figure 2: The 3D velocity field v = (v1, v2, v3) in the three-dimensional space (x1, x2, x3).

Key Mathematical Challenges:

• Forward Problem: Calculating the external field generated by a known source within the brain.
• Inverse Problem: Determining the source of brain activity from measured external fields.

The study demonstrates that solving these problems requires advanced mathematical modeling, including ellipsoidal harmonics and Lamé functions.

2. Creeping Hydrodynamics (Stokes Flow)

In fluid mechanics, Stokes flow refers to the flow of fluids with very low Reynolds numbers, where viscous forces dominate over inertial forces. The study presents mathematical models for solving boundary value problems involving particles in fluid flows.

Applications in Mathematics and Engineering:

• Particle-In-Cell Models: Used to simulate the motion of particles in fluids.
• Happel-Type Boundary Conditions: A method to simplify complex fluid flow problems.

The study highlights the use of ellipsoidal geometry to model particles of arbitrary shapes, which is crucial for understanding fluid dynamics in various engineering applications.

3. Identification of Metallic Bodies in Conductive and Lossless Media

The study also explores the identification of metallic bodies embedded in different media, such as Earth’s subsurface or air cavities. These problems are essential in fields like geophysics, electromagnetic imaging, and security scanning.

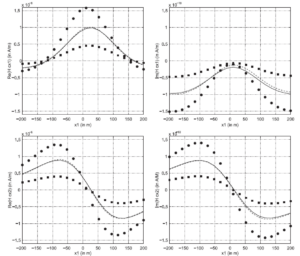Figure 3: Real (left column) and imaginary (right column) parts of the magnetic field scattered by several metallic bodies. The third components all vanish due to the position of the magnetic dipole.

Mathematical Techniques Used:

• Low-Frequency Electromagnetic Scattering: Modeling the interaction between electromagnetic fields and metallic objects.
• Laplace and Poisson Equations: Solving these equations in ellipsoidal coordinates to predict the behavior of scattered fields.

The study demonstrates how mathematical models can be used to detect and identify metallic objects with high accuracy.

The Importance of Ellipsoidal Geometry in Mathematics

Why is ellipsoidal geometry important? Unlike simpler shapes like spheres or cylinders, ellipsoids can more accurately represent the shapes of real-world objects. This makes them essential for modeling complex systems in Mathematics and related fields.

For example:

• The human brain can be approximated as an ellipsoid for EEG and MEG studies.
• Particles in fluid flows are often better modeled as ellipsoids than spheres.
• Metallic bodies in electromagnetic studies are often ellipsoidal in shape.

The study highlights that solving boundary value problems in ellipsoidal geometry requires specialized mathematical tools, but the results are more applicable to real-world scenarios.

Future Directions in Boundary Value Problems and Mathematics

The study suggests several future directions for research in Mathematics related to boundary value problems in ellipsoidal geometry:

1. Developing More Efficient Numerical Methods: Improving computational techniques to solve boundary value problems more efficiently.
2. Exploring New Applications: Applying ellipsoidal boundary value problems to emerging fields like quantum computing and nanotechnology.
3. Integrating Machine Learning: Using machine learning algorithms to predict solutions to complex boundary value problems.

These future directions highlight the ongoing importance of Mathematics in solving real-world problems through advanced modeling techniques.

Conclusion

The study “Boundary Value Problems in Ellipsoidal Geometry and Applications” provides valuable insights into the role of Mathematics in solving complex boundary value problems. By applying advanced mathematical tools like ellipsoidal harmonics and Lamé functions, researchers can tackle challenges in brain imaging, fluid mechanics, and electromagnetic scattering.

For more insights, explore the full study: Full Text | PDF

Mathematics continues to be at the forefront of scientific and technological advancements, offering solutions to some of the most pressing challenges in modern society.